√100以上 三角 関数 積 145108-三角関数積分 漸化式
三角関数の乗積には興味深い性質がある。 それを利用して厳密な階乗の式を導く。 sin 関数の乗積では Π k=1 n1 2sin( π k/n)=n が成り立つ。三角関数の積 (1) \ \prod_{k=1}^{n1}\sin\frac{k\pi}{n}=\frac{n}{2^{n1}} \ (2) \ \prod_{k=1}^{n1}\cos\frac{k\pi}{n}=\frac{\sin\left(\frac{n\pi}{2}\right)}{2三角関数和→積の公式 mixiユーザー 08年06月18日 1705 三角関数を因数分解したり、積分するときに必要となる和を積(その逆)にする公式って面倒くさくありませんか?
積和公式の語呂合わせ 怜悧玲瓏 高校数学を天空から俯瞰する
三角関数積分 漸化式
三角関数積分 漸化式-本記事では、三角関数の公式のうち、「積和の公式」「和積の公式」とその証明について記述する。 目次 1 積和の公式11 積和の公式一覧12 sin 〇 cos の式13 cos 〇 sin の式14 cos 〇 cos の式1Mar 06, 21 · 三角関数の和積,積和公式 三角関数の「和」を「積」に直したり,「積」を「和」に直す公式です。公式を丸ごと覚えるのではなく,導出の流れを覚えておくのがおすすめです。


三角関数の積と和の公式 思考力を鍛える数学
三角関数は周期関数なので、逆関数は多価関数である。 逆関数の性質から以下が成り立つ: =,() = − / ≤ ≤ /ピタゴラスの定理 ピタゴラスの定理やオイラーの公式などから以下の基本的な関係が導ける 。 = ここで sin 2 θ は (sin(θ)) 2 を意味する。 この式を変形して、以下の式が導かれる:三角関数(さんかくかんすう、英 trigonometric function )とは、平面三角法における、角の大きさと線分の長さの関係を記述する関数の族および、それらを拡張して得られる関数の総称である。 鋭角を扱う場合、三角関数の値は対応する直角三角形の二辺の長さの比(三角比)である。三角形における三角関数の等式の証明(和積の公式を利用) 三角関数のsin型合成 asinθbcosθ=rsin(θα) とcos型合成;
三角関数・和積の公式です。 問:sin10°sin50°sin250°の値を求めよ。 ちなみに答えは0、私はこの問題を以下のように解きました。 和積の公式より、 sin10°sin50°sin250° =2sin30°sin(°)sin250° =sin°sin250° ここで、sin°は、sin250°はなので答えの0と合わないことがわかります今回は 三角関数・三角関数の逆数・逆三角関数・双曲線関数 の微積を確認していきます。ですので、今回は全く面白くないです。 とりあえず、公式一覧を載せてしまいましょう。公式の証明などはそのMay 26, · 三角関数の積和・和積の公式は、形が合計で8つもあり、覚えるのが難しい公式ですよね。そこでこの記事では、積和・和積の公式の覚え方・証明・使いどころを紹介します。和積・積和公式で難しいのは見かけだけなので、語呂合わせで覚えてしまいましょう!
応用分野: べき級数, 三角関数の不等式の解き方, 三角方程式の解き方, 三角関数 和積の公式, 次数下げの基本式, 加法定理, 問題リスト ←このページに関連している問題です三角関数(グラフ) sin、cos、tanの関数表を計算し、sinとcosのグラフを表示します。 逆三角関数(度) アークサイン、アークコサイン、アークタンジェントなどの逆三角関数を度単位で計算します。 角度と底辺から斜辺と高さを計算§3 多重三角関数 多重三角関数は三角関数(双曲型三角関数を考えるとわかりやすい)いくつ かから多重化して得られたものです。これは、一般の多重ゼータ関数より明快 ですので、そこを重点的に講義したのが1991年の4月-7月に東京大学


三角関数の公式


三角関数の公式 図的理解
三角関数で表された関数の場合,$\boldsymbol{t=\tan \dfrac{x}{2}}$ とした置換積分が有効です. ※ ここに詳しくは書けませんが有理関数の積分は少なくとも大学範囲の知識を使えば必ずできるので,三角関数を有利関数表示をすることに意味があります.Mar 06, 21 · 三角関数の積和公式は丸覚えするのではなく,自力で素早く導出できるようにしておくことを推奨します。 公式そのものではなく以下の手順を覚えましょう。 素早く導出する方法 step0.三角関数の加法定理(a)~(d)をきちんと覚える。 step1.作りたいもの=とMay , 18 · 標準三角関数の積から和への公式では、三角関数の積を、和や差に分解する式を見ました。ここでは、逆に、和を積にする式を見ていきます。 どちらかというと、当面は和から積に変換することが多いです。例えば、ある三角関数の和が $0$ になるとき


第2章 三角関数



高校数学 三角方程式 不等式 三角関数の和積の公式 受験の月
1 指数関数と三角関数 指数関数et はtで微分したものが元の関数と同じになる関数であり、tのべき級数で表すと et = 1t 1 2 t2 1 3·2 t3 1 4·3·2 t4 ··· となる。他方、虚数i (ここでiは虚数単位、 は実数)を引数とする指数関数ei は複素面上の半径三角関数を扱う場合には,積分に限らず次数に注目する必要があります。なぜなら,2倍角の公式や3倍角の公式 \\begin{array}t{l} \sin 2x = 2 \sin x \cos x \\ \cos 2x \begin{array}t{l} = \cos^2 x \sin^2 x \\ = 2\cos^2 x 1 \\ = 1 2\sin^2 x \end{array} \\ \displaystyle \tan 2x = \frac{2 \tan x}{1 \tan^2 x} \\8px \cos 3x = 4 \cos^3 x 3 \cos複素関数1 微分 三角関数 指数対数関数 複素数における微分、三角関数、指数関数、対数関数の性質のまとめです。 実数の場合とはかなり異なる性質も多くあります。 ※複素関数の一覧はこちら 微分



3分で分かる 三角関数の積和 和積の公式の覚え方 証明 使いどころをわかりやすく 合格サプリ



2 Sin 75sin 152sindfrac Lihat Cara Penyelesaian Di Qanda
三角対数と対数関数の積(芸術的な関数?), Excel と VBA を用いた数学実験ブログです。 Excel の機能を使って色々な関数のグラフを描いています。 ブログの片隅に「こばとちゃんの数学コーナー」もあります。 ≫ 姉妹サイトにて「数論講座」連載中!Mar 06, 21 · 三角関数の積の積分で重要なのは定積分ですが,とりあえず不定積分をやってみます。 例 ∫ cos 3 x cos 4 x d x \displaystyle\int\cos 3x \cos 4xdx ∫ cos 3 x cos 4 x d xる3, p92.このような無限積において,本論文の前半では,例に挙げたような三角関数 の無限積表示やその性質,また,z のべき指数と自然数の2進数,3進数表示との関連を 考察した.前半の主な結果は次の二つの定理である. 定理11 (A) ∏1 k=0 (1z 3k z2 3k



加法定理 和と差の変換の問題 高校数学に関する質問 勉強質問サイト


三角関数の積と和の公式 思考力を鍛える数学
Mar 06, 21 · 重要なのは,この公式を丸々覚えることではなく, 三角形の内角の三角関数の和は積に,積は和に変換できる という事実を覚えておき,その場で導出できるようになっておくことです。 ちなみに, a b c = π abc=\pi a b c = π でなくて a b c = 2 π abc=2\pi a b c = 2 π のときなども同様な三角関数 積和の公式 ページトップ(17)(18)は被積分関数が偶関数であるから,(14)(15)の半分になる. (19)← 三角関数の積を和に直す公式 により ア) の両方が奇数または両方が偶数のとき, は偶数になる



三角関数 積和の公式 和積の公式 忘れていたら即クリック 高校生向け受験応援メディア 受験のミカタ



高校数学 三角関数の積和 和積の公式の証明 受験の月
和積(4)の公式の証明 cos( ) = cos cos sin sin ) cos( ) = cos cos sin sin cos( ) cos( ) = 2sin sin ) cos A cos B = 2sin A B 2 sin A B 2 = A;三角関数 和積の公式 KIT 金沢工業大学 ページトップ三角関数の導関数(微分) 三角関数の積分 演習問題 質問解答集には三角関数に関する問題もあります.大変役に立ちますよ. ホーム>>カテゴリー別分類>>三角関数 最終更新日 年6月6日


Lesson1 Html



三角関数の和積 積和公式の簡単な導き方 さしあたって
三角関数の方程式について、2種類の解き方で解いてみましょう。 問題 box03 title="三角関数の方程式"$0 三角関数の方程式(3倍角・和積公式の利用)|オンライン予備校 eYOBI ネット塾



数 不定積分のまとめと解き方 Part9 三角関数を含む積分の基本 すうじょうさん Note


三角関数の乗積と階乗


三角関数の積と和の公式 思考力を鍛える数学



和積 積和 変換公式 おいしい数学



数学 三角関数 半角の公式 オンライン無料塾 ターンナップ



三角関数の無限乗積展開 理系ノート


三角関数 Of 京極一樹の数学塾会員頁
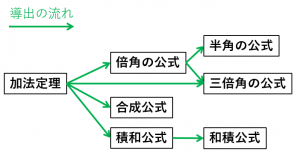


三角関数の加法定理に関する公式全22個 導出の流れつき 具体例で学ぶ数学



加法定理 倍角公式 積和公式等



回転移動を表す行列 三角関数の加法定理の証明へ 身勝手な主張



三角関数の公式まとめ 倍角 半角 合成 Wolfram Alphaを使って数学を勉強しよう



入門 三角関数の和積 積和公式 導出 例題 Tetsu Lab
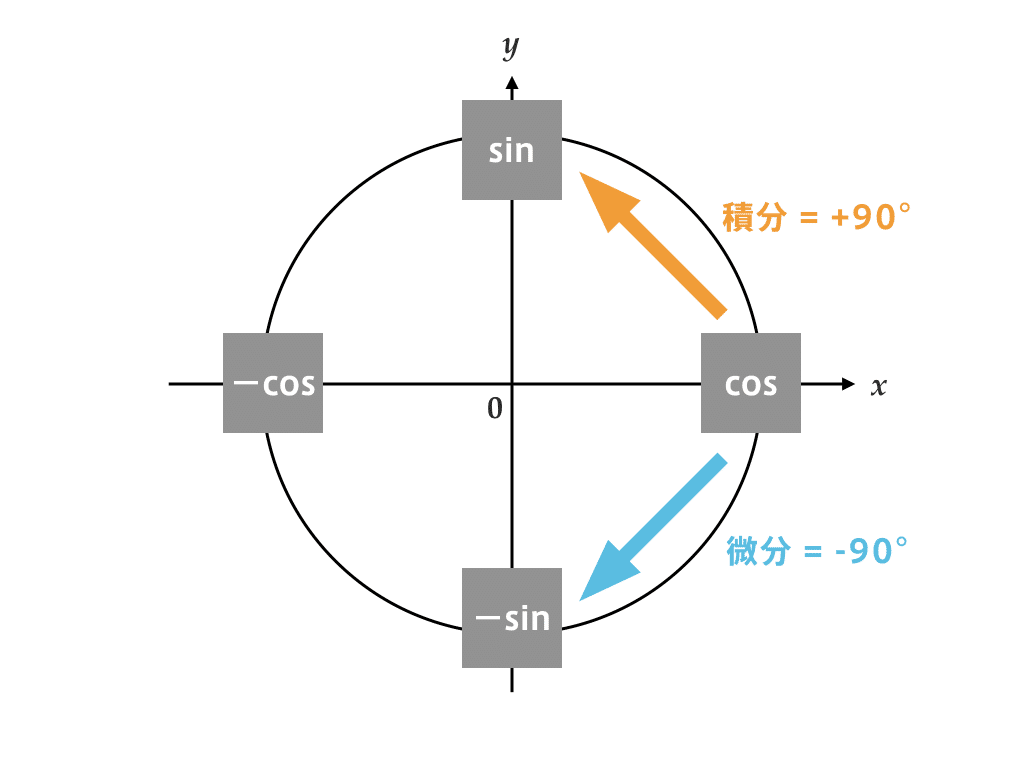


三角関数の微分 積分の覚え方 関谷 翔 Note



加法定理 倍角公式 積和公式等



三角関数 積和の公式 和積の公式 忘れていたら即クリック 高校生向け受験応援メディア 受験のミカタ


三角関数の公式 図的理解



三角関数の積和 和積公式 三変数版 香料ゐっすゐの夢



三角関数 積和の公式を使った問題が途中から分かりません 高校数学に関する質問 勉強質問サイト


三角関数の積分 京極一樹の数学塾



Sin Cos の区分求積法 高卒で大学数学



3分で分かる 三角関数の積和 和積の公式の覚え方 証明 使いどころをわかりやすく 合格サプリ



三角関数の積和 和積の公式 電気の神髄



保存版 高校数学 三角関数 和積 積和の公式 暗記法と導出法 加法定理から導く Sacramy



3分で分かる 三角関数の積和 和積の公式の覚え方 証明 使いどころをわかりやすく 合格サプリ


複素数と三角関数



和積 積和の公式のわかりやすい覚え方と証明のコツ



勉強しよう数学 三角関数の和と積の公式



数学得意な方お願いします 和 積の公式を初めて知りました これって暗記ですか Clear


積和公式の語呂合わせ 怜悧玲瓏 高校数学を天空から俯瞰する
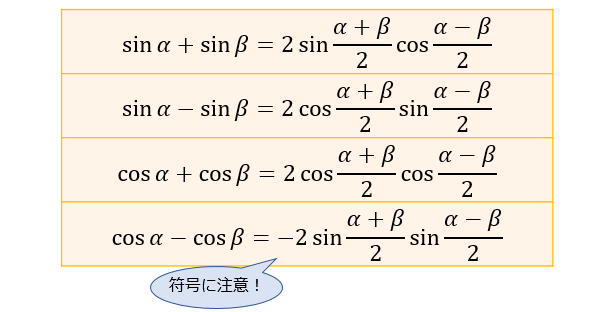


三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ



勉強しよう数学 三角関数の和と積の公式
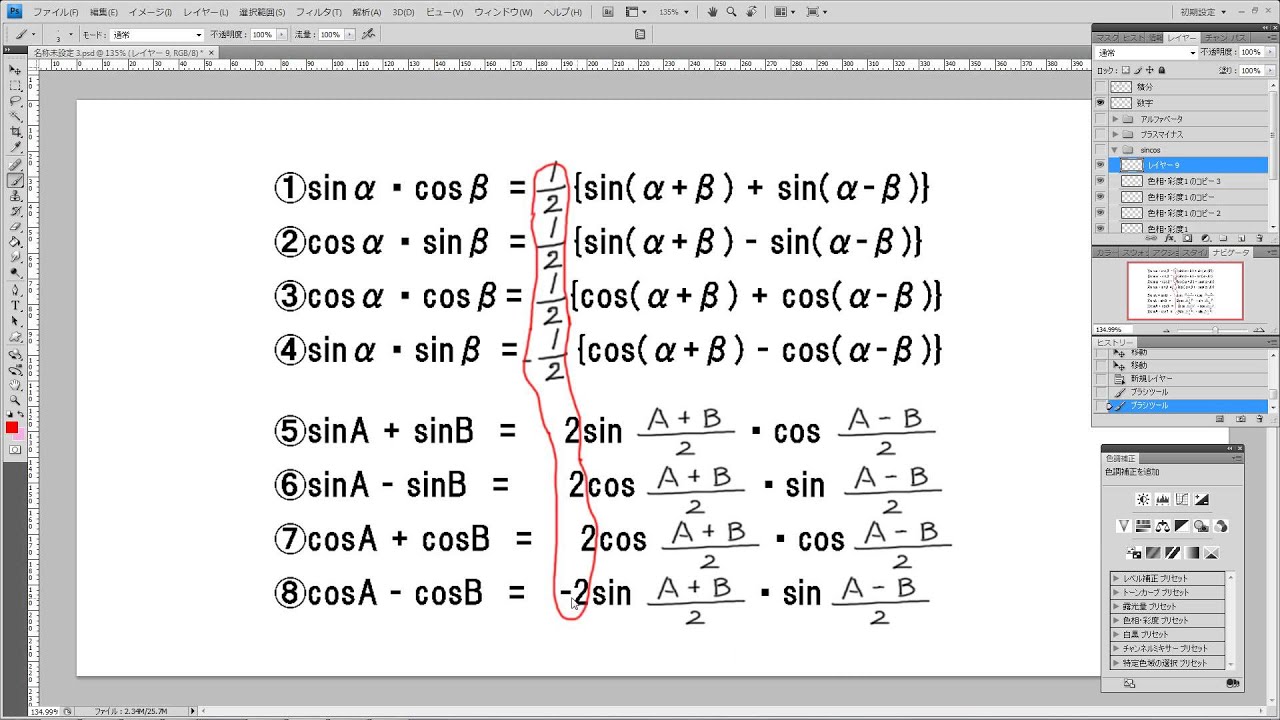


積和 和積の公式の簡単な覚え方 超簡単 Youtube



三角関数の微分 公式の証明と例題 高校生向け受験応援メディア 受験のミカタ



三角関数の積分法17 2 積和公式5秒とか無理くね 怜悧玲瓏 高校数学を天空から俯瞰する



和積の公式 覚え方 導き方 理系ラボ



三角関数の積和の公式について 高校数学の達人 河見賢司の日記
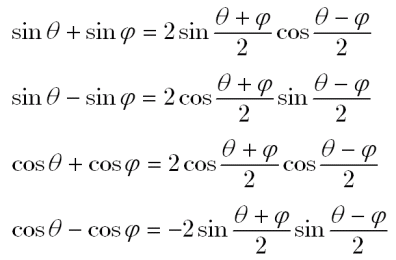


三角比 積和公式 和積公式は何に使うのか 大人が学び直す数学



積和 和積公式まとめ 理系ノート



うなり と 和積公式 岡竜之介のブログ



問題 解答 三角関数和積の公式問題 Gooブログはじめました



勉強しよう数学 三角形の垂心の図の全ての線分を三角関数の積で表す



三角関数の半角 2倍角 3倍角 和積 積和の公式を伝授します


三角関数の和と積の公式の証明 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開



三角関数の公式の覚え方と導出のコツ一覧 丸暗記不要
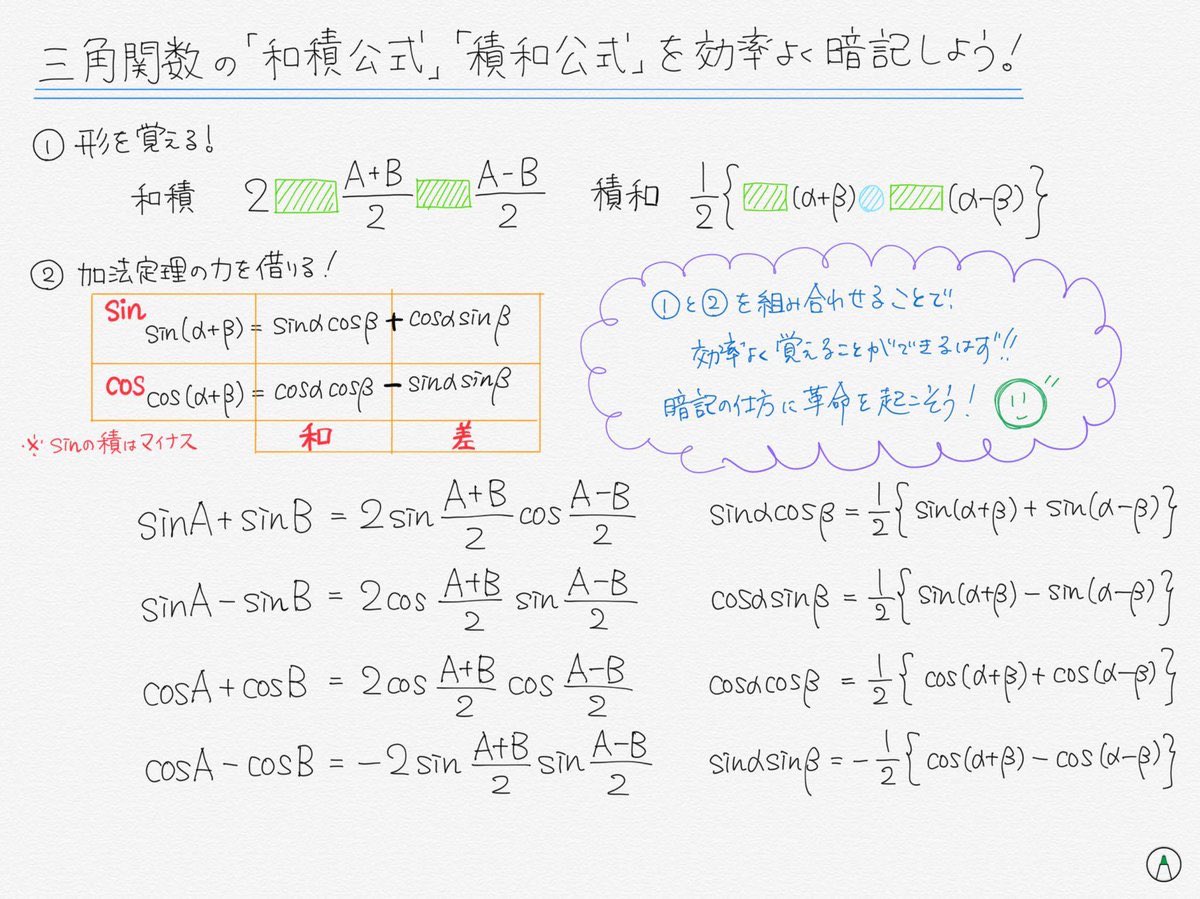


Avainsana 積和公式 Twitterissa



三角関数 積和公式 和積公式 Canada S Windview



微分積分学 4回目



和積公式の語呂合わせ2016 怜悧玲瓏 高校数学を天空から俯瞰する


三角関数の乗積と階乗



Avainsana 積和公式 Twitterissa



和積 積和の公式 数学の偏差値を上げて合格を目指す



加法定理 倍角公式 積和公式等



和積の公式はわかります 演習問題57です 和積の公式をどう使 高校数学に関する質問 勉強質問サイト


三角関数の積分 京極一樹の数学塾


高校数学 三角関数の積分 文字を含む三角関数の積の定積分 受験の月


三角関数の直交性 1



3分で分かる 三角関数の積和 和積の公式の覚え方 証明 使いどころをわかりやすく 合格サプリ



ねこ騙し数学



数2bの三角関数についてです 和積の公式の証明についてですが A B 数学 教えて Goo



三角関数の公式の一覧 Wikipedia



三角関数の公式 加法定理から積和 和積公式 三角関数の合成まで Irohabook



積和公式 数学 B 三角関数 Youtube


三角関数の直交性 1



三角関数の積和 和積の公式 電気の神髄



数 三角関数の式の値 漠然とした質問なのですが Clear



加法定理 倍角公式 積和公式等



三角関数の半角 2倍角 3倍角 和積 積和の公式を伝授します



三角関数の積分法1 積和公式を使うシリーズ 怜悧玲瓏 高校数学を天空から俯瞰する


三角関数の積と和の公式 思考力を鍛える数学



数学 B 三角関数の和積公式と積和公式 北見工業大 首都大学東京 大学入試数学の考え方と解法



三角関数の和 差 を積に直す公式の証明とその応用


コイン250枚以下の三角関数の無限乗積展開 を導出してく Yahoo 知恵袋



和積 積和の公式のわかりやすい覚え方と証明のコツ


三角関数の公式 図的理解



部分積分法の公式の証明と くり返し部分積分 のやり方 アタリマエ



三角関数は2時間で解けるようになる 外資系コンサルタントが主夫になったら



コサインの3つの和の値と3つの積の値 三角関数8 数学検定1級はこれだけで合格できる



三角関数の公式の一覧 Wikipedia



共通テスト対策シリーズ 三角関数の積和公式 和積公式 Youtube
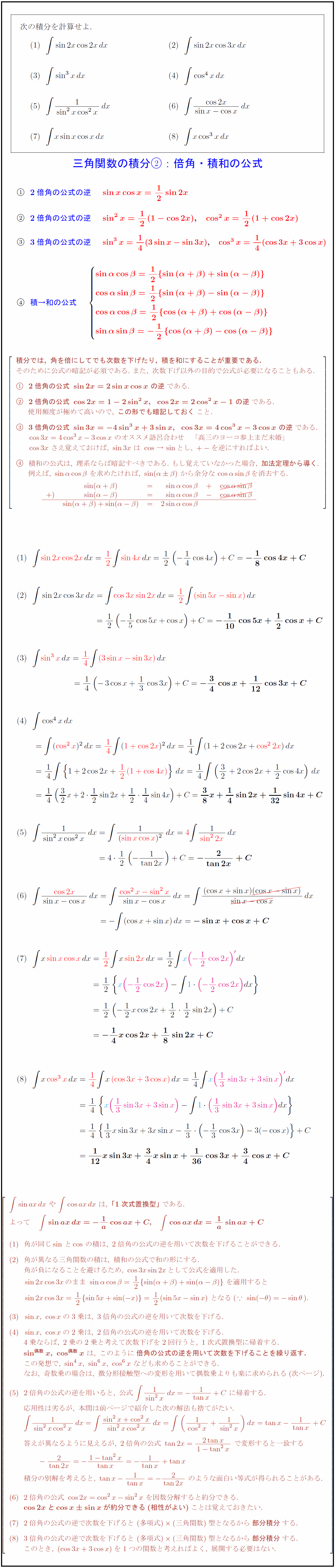


高校数学 三角関数の積分 2倍角 3倍角 積和の公式の利用 受験の月


和積公式の語呂合わせ 怜悧玲瓏 高校数学を天空から俯瞰する
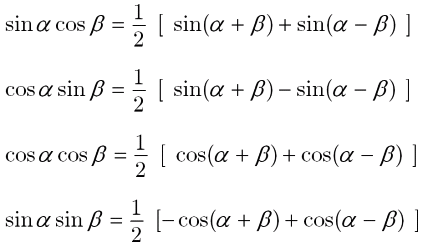


三角比 積和公式 和積公式は何に使うのか 大人が学び直す数学
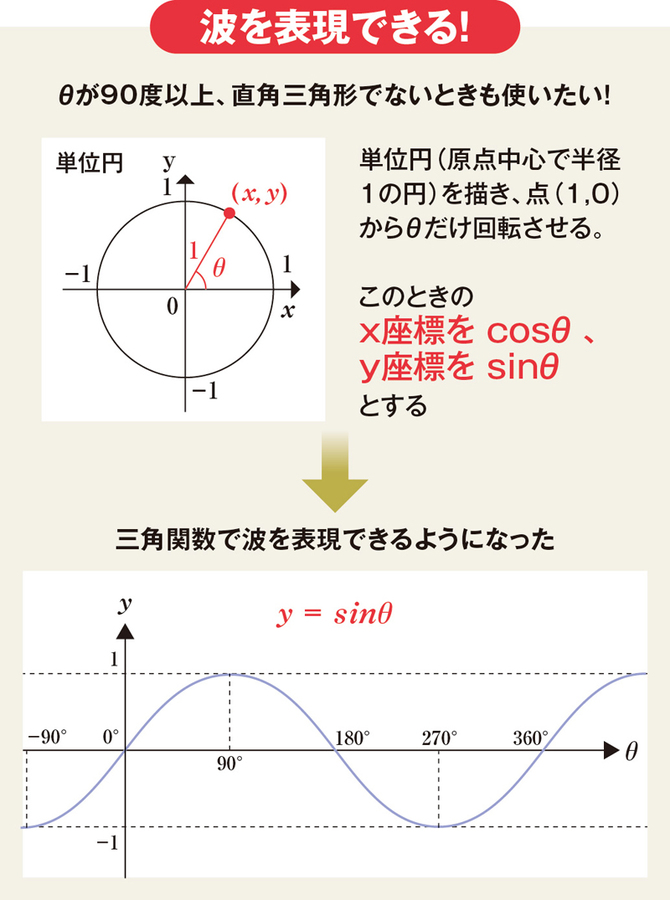


家電やスマホに必須 三角関数は陰の働き者 中高数学おさらい 三角関数 数列 文系でも怖くない 学び直し 数学 ダイヤモンド オンライン



三角関数の和と積の公式の証明 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開



三角関数の和と積の公式の問題で 下から2行目の部分の計算過程が分かりません Clear



三角関数2 積 和 和 積の公式の証明 Youtube



数 不定積分 三角関数 積和公式 オンライン無料塾 ターンナップ Youtube


三角関数の公式


コメント
コメントを投稿